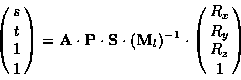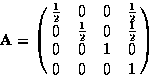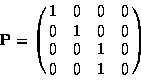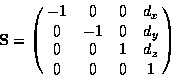Next: 11.2.2.2 Using Dual-Paraboloid Maps
Up: 11.2.2 Dual-Paraboloid Environment Mapping
Previous: 11.2.2 Dual-Paraboloid Environment Mapping
The principle that underlies paraboloid maps is the same principle that
underlies a parabolic lens or satellite dish. The geometry of a
paraboloid can focus rays. The paraboloid used for dual-paraboloid mapping is:
Figure 74 shows how two paraboloids can focus
the entire environment surrounding a point into two images.
Unlike the sphere mapping approach that the encodes the entire environment
in a single texture, the dual-paraboloid mapping scheme requires two textures to
store the environment, one texture for the ``front'' environment
and another texture for the ``back'' environment. Importantly, the
sense of ``front'' and ``back'' is completely independent of the
viewer orientation. Figure 75 shows an example of
two paraboloid maps.
Because two textures are required, the technique
must be performed in two rendering passes though this can be reduced
to a single rendering pass if multitexturing is supported.
Because the math for the paraboloid is all linear (unlike the spherical
basis of the sphere map), Heidrich and Seidel observe that OpenGL with
its texture matrix can map a eye-coordinate
reflection vector 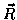 into a 2D texture coordinate (s,t)within a dual-paraboloid map.
Construct the necessary texture matrix as follows:
into a 2D texture coordinate (s,t)within a dual-paraboloid map.
Construct the necessary texture matrix as follows:
where
is a matrix that scales an biases a 2D coordinate in the range [-1,1] to the
texture image range [0,1]. And where
is a projective transform that divides by the z coordinate. This
serves to flatten a 3D vector into 2D. And where
is a matrix that subtracts the supplied 3D vector from an orientation
vector 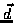 that supplies a view direction. We will make
that supplies a view direction. We will make 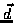 either
(0,0,-1)T or
(0,0,1)T depending on whether we are mapping the
front or back paraboloid map respectively. Finally, the matrix
either
(0,0,-1)T or
(0,0,1)T depending on whether we are mapping the
front or back paraboloid map respectively. Finally, the matrix
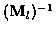 is the inverse of the linear part of the current (affine) modelview matrix.
The matrix
is the inverse of the linear part of the current (affine) modelview matrix.
The matrix
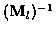 transforms a 3D eye-space reflection vector into
an object-space version of the vector.
transforms a 3D eye-space reflection vector into
an object-space version of the vector.




Next: 11.2.2.2 Using Dual-Paraboloid Maps
Up: 11.2.2 Dual-Paraboloid Environment Mapping
Previous: 11.2.2 Dual-Paraboloid Environment Mapping
David Blythe
1999-08-06

![]() into a 2D texture coordinate (s,t)within a dual-paraboloid map.
Construct the necessary texture matrix as follows:
into a 2D texture coordinate (s,t)within a dual-paraboloid map.
Construct the necessary texture matrix as follows: