We have discussed some of the caveats of using depth buffering, but there are several other aspects of OpenGL rasterization and depth buffering that are worth mentioning [2]. One big problem is that the rasterization process uses inexact arithmetic so it is exceedingly difficult to handle primitives that are coplanar unless they share the same plane equation. This problem is exacerbated by the finite precision of depth buffer implementations. Many solutions have been proposed to handle this class of problems, which involve coplanar primitives:
Many of these problems have elegant solutions involving the stencil buffer (Section 7.2, Section 3.5), but it is still worth describing alternative methods to get more insight into the uses of the depth buffer.
The problem of decaling one coplanar polygon into another can be solved rather simply by using the painter's algorithm (i.e., drawing from back to front) combined with color buffer and depth buffer masking, assuming the decal is contained entirely within the underlying polygon. The steps are:
Outlining a polygon and drawing hidden lines are similar problems. If we have an algorithm to outline polygons, hidden lines can be removed by outlining polygons with one color and drawing the filled polygons with the background color. Ideally a polygon could be outlined by simply connecting the vertices together with line primitives. This seems similar to the decaling problem except that edges of the polygon being outlined may be shared with other polygons and those polygons may not be coplanar with the outlined polygon, so the decaling algorithm can not be used, since it relies on the coplanar decal being fully contained within the base polygon.
The solution most frequently suggested for this problem is to draw the outline as a series of lines and translate the outline a small amount towards the eye. Alternately, the polygon could be translated away from the eye instead. Besides not being a particularly elegant solution, there is a problem in determining the amount to translate the polygon (or outline). In fact, in the general case there is no constant amount that can be expressed as a simple translation of the z object coordinate that will work for all polygons in a scene.

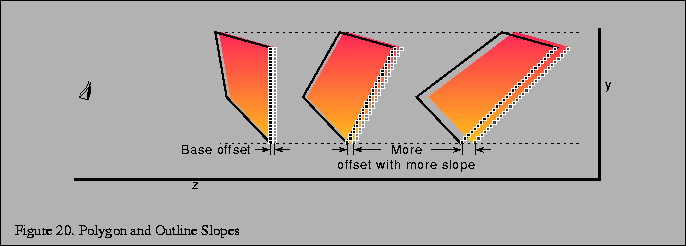
Figure 20 shows two polygons (solid) with outlines (dashed) in the screen space y-z plane. One of the primitive pairs has a 45-degree slope in the y-z plane and the other has a very steep slope. During the rasterization process the depth value for a given fragment may be derived from a sample point nearly an entire pixel away from the edge of the polygon. Therefore the translation must be as large as the maximum absolute change in depth for any single pixel step on the face of the polygon. The figure shows that the steeper the depth slope, the larger the required translation. If an unduly large constant value is used to deal with steep depth slopes, then for polygons which have a shallower slope there is an increased likelihood that another neighboring polygon might end up interposed between the outline and the polygon. So it seems that a translation proportional to the depth slope is necessary. However, a translation proportional to slope is not sufficient for a polygon that has constant depth (zero slope) since it would not be translated at all. Therefore a bias is also needed. Many vendors have implemented the EXT_polygon_offset extension that provides a scaled slope plus bias capability for solving outline problems such as these and for other applications. A modified version of this polygon offset extension has been added to the core of OpenGL 1.1 as well.