To smoothly shade an object, the same normal should be used on a given vertex for all polygons that share the vertex. The simplest way to do this is to add all (normalized) normals from the common facets then renormalize the result [38]. This provides reasonable results for surfaces that are fairly smooth, but does not look good for surfaces with sharp edges.
An object with a sharp corner, such as a cube, should look like it has a hard edge, rather than a soft edge. The angle between polygons that should produce a hard edge can vary from model to model. It is fairly clear that a 90 degree edge should always be considered a hard edge, but some models look better with hard edges at angles less than 45 degrees while others look better with soft edges for angles greater than 45 degrees. This particular parameter should generally be left under user control with a good default probably right around 45 degrees.
To determine the angle between polygons, take the dot product of the facet normals (which must be unit length). A dot product returns the cosine of the angle between the vectors. So, if the dot product of the two normals is greater than the cosine of the desired hard edge angle, the edge should be considered soft, otherwise it should be considered hard. To create a hard edge, a different normal is generated for each side. Be sure to keep common normals for any remaining soft edges of the surface.

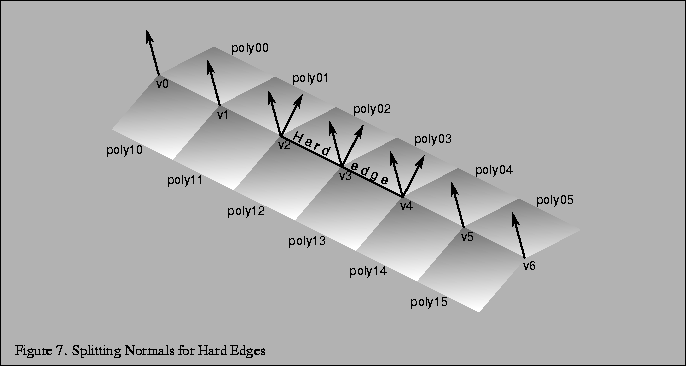
Figure 7 shows an example of a mesh with two hard edges in it. The three vertices making up these hard edges, v2, v3, and v4, need to be split using two separate normals. In the case of vertex v2, one normal would apply to poly01 and poly02 and a different normal would apply to poly11 and poly12. This makes sure that the edge between poly01 and poly02 still looks smooth while the edge between poly02 and poly12 has a nice crease and looks like a sharp edge. Since v1 is not split, the edge between poly01 and poly11 will look sharper near v2 and will become smoother as it gets closer to v1. The edge between v1 and v0 would then be completely smooth. This is the desired effect.
For an object such as a cube, three hard edges will share one common vertex. In this case the edge splitting algorithm needs to be repeated for the third edge to achieve the correct results.