11.1.2 Planar Reflectors

This section discusses the modeling of planar reflective surfaces. Three techniques are discussed: using the stencil buffer to draw the reflected geometry in the proper location, a technique using OpenGL's clip planes to clip reflected geometry to a reflected space visible by the eyepoint, and a technique which uses texture mapping to make an image of the reflected geometry which is then texture mapped onto the reflective polygon. Both techniques construct the scene in two (or more) passes.

As an example, consider a model of a room with a mirror on one wall. Compute the plane containing the mirror and define an eye point from which to render the scene. When drawing the reflected scene, first apply a transformation that reflects objects across this plane. This can be envisioned as either reflecting the eye point or the objects across the plane; both are identical and some people find one approach more intuitive than the other.

The reflection transformation can be decomposed for convenience into a translation to the origin, a rotation mapping the mirror into the XY plane, a scale of -1 in Z, the inverse of the rotation previously used, and a translation back to the mirror location.

Given one vertex P of the planar reflector and a vector $\vec{V}$ perpendicular to the plane, this sequence of transformations can be expressed as the single 4 by 4 matrix R [34] shown below:

$$R = \pmatrix{ 1 - 2V_{x}^2 & -2V_{x}V_{y} & -2V_{x}V_{z} & 2... ...{z} & 1 - 2V_{z}^2 & 2(P \cdot V) V_{z} \cr 0 & 0 & 0 & 1\cr}$$

where

$$P \cdot V = P_{x}V_{x} + P_{y}V_{y} + P_{z}V_{z}$$

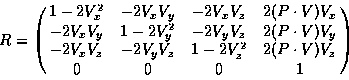
Applying this transformation to the original scene produces a virtual scene on the opposite side of the reflector representing the reflected scene. The next sections discuss how to render this reflected scene correctly within the non-reflected scene.