Next: 10.7 Bump Mapped Reflections
Up: 10.6 Bump Mapping with
Previous: 10.6.0.7 Bumps on Surfaces
Although this technique does closely approximate bump mapping,
there are limitations that impact its accuracy.
- Bump Map Sampling
- The bump map height function is not continuous, but
is sampled into the texture. The resolution of the texture affects how
faithfully the bump map is represented. Increasing the size of the bump map
texture can improve the sampling of the high frequency height components.
- Texture Resolution
- The shifting and subtraction steps produce the
directional derivative. Since this is a forward differencing technique,
the highest frequency component of the bump map increases as the shift is
made smaller. As the shift is made smaller, more demands are made of the
texture coordinate precision. The shift can become smaller than the
texture filtering implementation can handle, leading to noise and aliases
effects. A good starting point is to size the shift components so their
vector magnitude is a single texel.
- Surface Curvature
- The tangent coordinate axes are different at
each point on a curved surface. This technique approximates this by
finding the tangent space transforms at each vertex. Texture mapping
interpolates the different shift values from each vertex across the polygon.
For polygons with very different vertex normals, this approximation can
break down. A solution would be to subdivide the polygons until their
vertex normals are parallel to within some error limit.
- Maximum Bump Map Slope
- The bump map normals used in this technique are
good approximations if the bump map slope is small. If there are steep
tangents in the bump map, the assumption that the perturbed normal is length
one becomes inaccurate, and the highlights appear too bright. This can
be corrected by creating a fourth pass, using a modulating texture derived
from the original bump map. Each value of the texel is one over the length of
the perturbed normal:
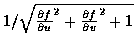




Next: 10.7 Bump Mapped Reflections
Up: 10.6 Bump Mapping with
Previous: 10.6.0.7 Bumps on Surfaces
David Blythe
1999-08-06