


  |
 |
Se comparado com o processo de visualização bidimensional, visto até o momento, a visualização de objetos tridimensionais é bastante mais complexa. Esta complexidade deve-se, basicamente, ao fato de que os dispositivos gráficos existentes são adequados à apresentação de imagens planas, bidimensionais.
PROJEÇÕES
Da mesma maneira que um desenhista, quando quer representar no papel a imagem de um objeto tridimensional, no computador também é preciso gerar uma projeção do objeto que se deseja exibir. Uma projeção nada mais é do que uma representação bidimensional de um objeto tridimensional.
A projeção é gerada por linhas de projeção que passam pelos vértices do objeto e atingem um plano de projeção.
Existem várias técnicas
e tipos de projeção, cada uma delas adequada a uma tipo de
aplicação. Nas figuras a seguir, estão as duas formas mais comuns de projeção.

Fonte: By SharkD - CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=58480268
Outro exemplo: https://www.quora.com/What-is-the-difference-between-orthographic-and-perspective-projections-in-engineering-drawing
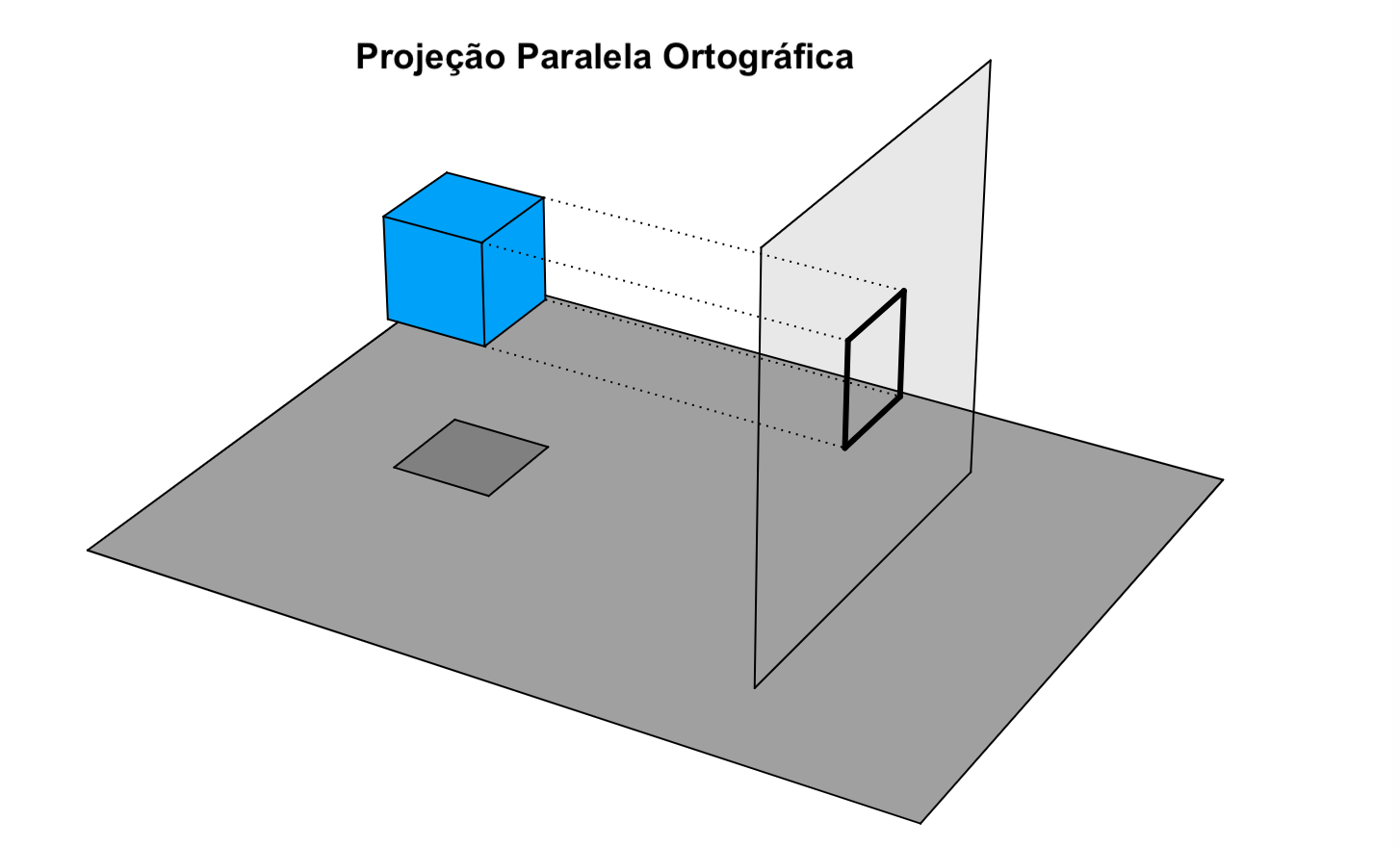
PROJEÇÃO PARAPELA ORTOGRÁFICA
Utilizada em engenharia, as linhas de projeção são paralelas entre si e perpendiculares ao plano de projeção.
Tipos mais comuns de
projeções ortográficas são: FRONTAL, LATERAL e SUPERIOR, nas quais o
plano de projeção é perpendicular aos eixos principais. Neste caso,
dado P = (x, y, z):

Figura - Exemplo da Projeção Paralela Ortográfica
Fonte: Profa. Isabel Harb Manssour
PROJEÇÃO PERSPECTIVA
Para a exibição realística de objetos, a projeção mais importante é a Perspectiva pois ela simula a projeção feita pelo olho humano quando este capta a imagem de um objeto.
A modelagem matemática da projeção perspectiva baseia-se nas seguintes noções básicas:
A figura 1 exemplifica as entidades mencionadas acima.

Figura 1 - Plano e Centro de Projeção
As coordenadas (Xp", Yp"), da projeção perspectiva P" de qualquer ponto P de coordenadas (Xp, Yp, Zp), colocado do lado oposto de CP, em relação ao plano de projeção PI, é obtido criando-se uma linha L de P até CP e calculando-se a intersecção desta com o plano PI. A figura 2 exemplifica o cálculo de P".

Figura 2 - A Projeção do Ponto P
O cálculo das coordenadas de P" é deduzido, de forma mais fácil, se a figura 2 for visualizada de 2 maneiras especiais:

Figura 3 - Vista Lateral Direita do Plano de Projeção
Da figura 3 pode-se retirar a seguinte relação, pela técnica de semelhança de triângulos:


Figura 4 - Vista Superior do Plano de Projeção
Da figura 4 pode-se retirar a seguinte relação, pela técnica de semelhança de triângulos:

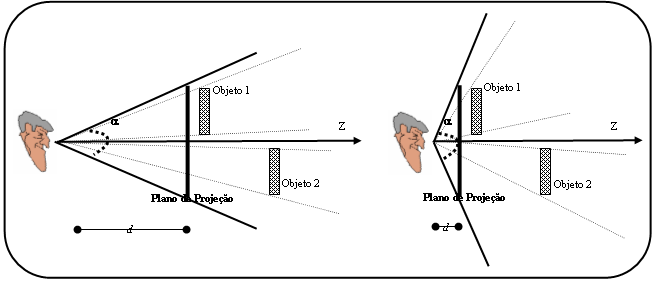
Como calcular o valor de "D" ?
O D da fórmula acima é a chamada Distância Focal, que é medida entre o centro de projeção e o plano de projeção, como mostram as figuras a seguir. Se o centro de projeção for posicionado próximo ao plano de projeção, os os objstos aumentam, do contrário, diminuem.
Além disso o
ângulo de visão define o quanto o observador consegue ver do universo,
e, em conseqüência, quanto do universo será exibido na tela. Este
ângulo funciona como o ângulo de abertura da lente de uma máquina
fotográfica, ou seja, quanto maior o ângulo, maior a região que pode
ser enquadrada na foto. Quando o ângulo for menor, e uma porção do
universo for visualizada, se tem o efeito de zoom.
Suponha que o plano de projeção tenha dimensões fixas formando um retângulo com extremos, por exemplo, em (-10, -10) e (10,10). Suponha, ainda, que se arbitre um ângulo de visão "alfa" que defina o quanto o observador consegue ver do universo, e em conseqüência, quanto do universo será exibido na tela. Este ângulo funciona como o ângulo de abertura da lente de uma máquina fotográfica, ou seja, quanto maior o ângulo, maior a região que pode ser enquadrada na foto.
Na vista lateral direita deste plano(figura 5). é possível deduzir uma fórmula para calcular o D.


Figura 5 - Cálculo do valor de D
O OBSERVADOR DO UNIVERSO
Outro componente importante no processo de visualização tridimensional em computadores, além das projeções, é a existência de um "observador virtual" das cenas. Este "observador" é quem define de que local deseja-se que a cena seja exibida, se de cima, de baixo, do lado esquerdo, do direito, etc.
A necessidade da existência deste observador explica-se pelo fato de que um mesmo conjunto de objetos no universo, visto de diferentes lugares tem, para quem os observa, diferentes coordenadas para cada posição. Por exemplo, suponhamos um cubo unitário(com arestas de tamanho 1) colocado com o centro na coordenada (10,10,10). Para um observador origem, as coordenadas do centro do cubo são também (10,10,10). Porém, se o observador for colocado na coordenada (10,0,0) o centro do cubo terá, em relação a ele as coordenadas (0,10,10).
Um ponto importante na definição do "observador virtual" é sua orientação, ou seja, para onde ele está olhando dentro do universo. Nos exemplos acima o observador foi tomado olhando na direção positiva do eixo Z. Porém, se invertermos esta orientação as coordenadas do centro do cubo se alterarão. Por exemplo, tomando o observador na origem e fazendo-o "olhar" na direção negativa do eixo Z, as coordenadas do centro do cubo passam a ser (-10,10,-10) pois o referido ponto ficará a sua esquerda, e a suas costas.
Pelo que foi exposto acima é preciso, então, definir a partir da posição do observador no universo e de sua orientação um novo sistema de referência, o chamado Sistema de Referência do Observador ou Sistema de Referência da Câmera(SRC) ou ainda Sistema de Referência de Projeção(SRP).
Assim sendo, antes de projetar qualquer entidade tridimensional é preciso obter suas coordenadas em relação ao SRC e somente então projetá-las.
A técnica matemática envolvida na obtenção
de coordenadas de um ponto em um novo sistema de referência vem da
Geometria Analítica e será aqui revisada sucintamente.
MUNDANÇA DE SISTEMA DE COORDENADAS(Mudança de Base)
Dado um sistema de coordenadas A, definido pelos vetores(eixos) i, j e k, com origem no ponto "O" e um 2º sistema, B, definido pelos eixos u, v e w, com origem em "O'", tem-se que, para obter as coordenadas de qualquer ponto P, no sistema B, dadas suas coordenadas no sistema A, a formulação é a seguinte:
O ponto P pode ser expresso por

onde,
[X, Y, Z] são as coordenadas do ponto P no sistema A e
[X', Y', Z'] são as coordenadas do ponto P no sistema B.
A obtenção das coordenadas de P no sistema B pode ser
feita simplesmente isolando o vetor [X',Y',Z'] na equação
acima.
SISTEMA DE REFERÊNCIA DA CÂMERA
Conforme já foi exposto, a definição do SRC é obtida a partir das coordenadas o observador e de sua orientação no universo.
Tomando o universo como o sistema de coordenadas cartesianas com origem em (0,0,0) e com vetores i=(1,0,0), j=(0,1,0) e k=(0,0,1) definido os eixos
do sistema, a expressão (1) pode ser simplificada da seguinte maneira:

que resulta em,

Já que O' pode ser expresso pelo ponto [Xo, Yo Zo] no universo temos a seguinte formulação para a equação (2),

que é equivalente a,

Como o que se deseja obter é a tripla[X',Y',Z'] basta isolá-la,
como segue:

Neste ponto surge a pergunta : "Como obteros vetores-eixos 'u', 'v' e 'w' ?
A componente "w" define o eixo Z do SRC e aponta na direção em que o observador está olhando. O cálculo de Z é feito pelo chamado VETOR ALVO(VA), que é definido como o segmento de reta orientado iniciando na posição do observador(Xo,Yo,Zo) e terminando no seu ponto de interesse(Xint, Yint, Zint).
w = [Xa Ya Za] = [Xint Yint Zint] - [Xo Yo Zo]
w = [Xa Ya Za] = [Xint-Xo Yint-Yo Zint-Zo]
A fim de facilitar futuros cálculos "w" deve ser um
vetor unitário e para isto basta diví-lo por seu módulo.
A figura 6 mostra a representação gráfica do Vetor-Alvo.

Figura 6 - Representação Gráfica do Vetor-Alvo
O Cálculo de "u":
O vetor "u" pode se calculado pelo
produto vetorial de VV pelo Vetor Alvo VA(Xa, Ya, Za). No caso, VV é um
vetor que define o "lado de cima"
do sistema de referência, e pode ser, por exemplo, (0,1,0).

que deve ser dividido por seu módulo, para ser tornado unitário, da seguinte forma:

O Cálculo de "v"
De forma similar ao que foi feito no caso de "u" a componente "w" pode ser calculada por um produto vetorial, desta feita VA x u

que também deve ser dividido por seu módulo, para ser
tornado unitário.
ATENÇÃO:
Se VA for igual a (0,1,0) haverá problema no cálculo de "u" pois o seu módulo valendo 0 irá impossibilitar a obtenção do vetor unitário. Uma solução para este problema é a "perturbação" da componente "x" de VA com um valor pequeno , por exemplo:
NOVO_VA = VA + [0.01 0 0]
OBTENÇÃO DAS CORDENADAS DE UM PONTO NO SRC
Partindo da formulação apresentada em (4) a obtenção das coordenadas de um ponto do SRU no SRC passa primeiro pelo cálculo da inversa da matriz de eixos do SRC.
Tomando as seguintes componentes simbólicas para "u", "v" e "w",
u=[abc], v=[def], w=[hij]
a matriz de eixos fica
a b c
d e f
h i j
cuja inversa é simplesmente sua transposta, pois o SRC forma uma base ortonormal. Base ortonormal é aquela em que todos os vetores que definem os eixos tem tamanho 1 e, além disso, são ortogonais entre si.
a d h
b e i
c f j
A partir da matriz obtida o cálculo é bastante trivial, resumindo-se a uma multiplicação de matrizes, conforme é apresentado a seguir.
[X' Y' Z'] = [X-Xo Y-Yo Z-Zo] a d h
b e i
Onde,
[X' Y' Z'] : Coordenadas do ponto no SRC
[Xo Yo Zo] : Coordenadas da posição do obsevador no SRU
[X Y Z ] : Coordenadas do ponto no SRU.
FIM