Disciplina de Computação Gráfica

Computação Gráfica
Processo de Visualização Bidimensional

INSTANCIAMENTO

INTRODUÇÃO

Em uma aplicação, muitas vezes, temos objetos que são derivados de um mesmo modelo, por exemplo: "numa planta baixa temos várias mesas, com a mesma estrutura básica, cada uma delas diferindo das outras apenas no tamanho, na cor e no posicionamento dentro da casa".

Quando uma situação deste tipo se apresenta diz-se que as "mesas" são instâncias de um mesmo modelo.

Instâncias, nada mais são do que alterações em modelos baseadas em parâmetros pré-definidos. A estes parâmetros costuma-se dar o nome de parâmetros de isntanciamento. Eles podem ser, por exemplo, tamanho, orientação, cor, material, etc.

Na figura a seguir é possível observar o uso de instâncias de três modelos("carro" e "avião"). No primeiro caso o "carro" é instanciado três vezes em posições diferentes. O "avião", instanciado 2 vezes, tem na primeira instância apenas sua posição alterada, na segunda também é alterada sua orientação.

Para armazenar as instâncias de uma aplicação pode-se usar, por exemplo, uma tabela contendo o nome do modelo e seus respectivos parâmetros de instanciamento. Tomando o universo da figura, pode-se armazenar as isntancias conforme a seguinte tabela.

Tabela - Armazenagem dos Parâmetros de Instanciamento

Modelo	POSX	POSY	ROT	ESC
Carro	....	....	....	....
Carro	....	....	....	....
Carro	....	....	....	....
Aviao	....	....	....	....
Aviao	....	....	....	....

Quanto aos modelos("carro" e "avião") usados para criar as instâncias, seu armazenamento pode ser feito de várias formas. Por exemplo, uma lista de retas ou até mesmo uma rotina. Esta última forma de armazenamento é bastante comum(e útil) especialmente quando se tem aplicações com um conjunto fixo de modelos. Um exemplo de uma aplicação deste tipo são os programas para a criação de circuitos lógicos. Neste caso os modelos(porta lógicas) são sempre os mesmos podendo, portanto, ser armazenados através de rotinas.

Por outro lado, em aplicações em que é possível criar ou alterar modelos a abordagem de armazenamento por listas é mais adequada. Na figura a seguir, apresenta-se a representação gráfica de um conjunto de modelos organizados em forma de listas.

Figura - Armazenamento de Modelos por Listas

Note que esta é apenas uma das inúmeras formas que podem ser utilizadas para armazenar modelos. As formas de armazenamento de modelos constituem um importante ramo da Computação Gráfica chamado Modelagem Geométrica que será explorado com mais detalhes em outro capítulo .

Pelo que foi visto acima existem duas principais vantagens na utilização de instâncias. São elas:

tornar o universo da aplicação menor pois para representar objetos diferentes basta armazenar o nome do modelo e os parâmetros de instanciamento, sem precisar repetir o modelo;
permitir um grande número de objetos diferentes a partir de um mesmo modelo.

SISTEMA DE REFERÊNCIA DO OBJETO

Na primeria figura foram apresentados, à esquerda, os modelos de um carro, de um avião e de uma bicicleta. Para facilitar a criação destes modelos foram foi adotado um espaço de coordenadas de (0,0) a (50,50). A este espaço de coordenadas, adequado à criação dos modelos dá-se, comumente, o nome de Sistema de Referência do Objeto.

Em outras palavras, o Sistema de Referência do Objeto, também chamado SRO, o sistema de coordenadas onde se define o modelo.

A escolha do tamanho do SRO é feita exatamente como está descrito acima: usa-se um sistema de coordenadas que facilite a criação do modelo.

TRANSFORMAÇÕES GEOMÉTRICAS

Os principais parâmetros de instanciamento utilizados em Computação Gráfica são as chamadas Transformações Geométricas de translação, rotação e escala. A seguir cada uma destas transformações será apresentada em detalhe.

Transformação de Translação

A translação define a posição do modelo no universo.

Dadas as coordenadas (xo,yo) de um ponto no SRO e os valores dos parâmetros de translação do modelo nos eixos X e Y (TX e TY), a obtenção do par de coordenadas correspondente (xu,yu), no SRU, é bastante simples:

xu= xo + TX
yu = yo + TY

É importante ressaltar, pelas características da fórmula recém apresentada, que o ponto do modelo que estiver sobre a origem do sistema de coordenadas será transferido, após a translação, para o ponto (TX,TY) do universo.

Esta característica é muito importante, e em geral, é considerada na criação de modelos com o objetivo de que se possa posicioná-los no universo da melhor forma possível. A figura 7.4 apresenta dois modelos de uma casa aos quais são aplicados os mesmos parâmetros de instanciamento. Note-se que a única diferença entre os modelos é a posição destes no SRO.

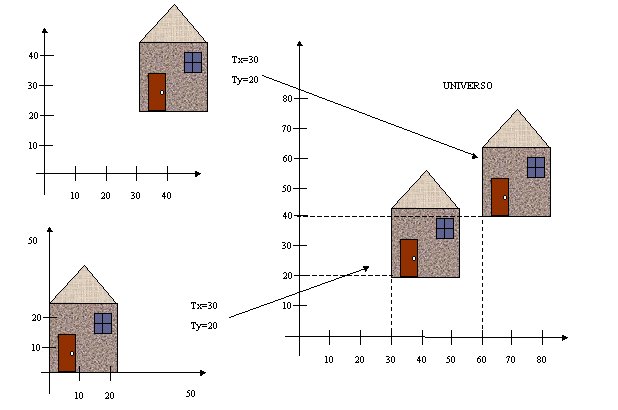
Figura - Exemplos de Translação

Transformação de Escala

A transformação de escala consiste da alteração do tamanho do modelo. A fórmula de "escalamento" de um ponto é a seguinte:

xu= xo * EX
yu = yo * EY

Onde EX e Ey são respectivamente os fatores de escala em relação aos eixos X e Y.

Sobre a transformação de escala é importante ressaltar algumas características:

a escala ocorre sempre em torno da origem do SRO. Isto quer dizer que todo o ponto que estiver sobre a origem, no SRO, permanece nesta posição após a escala. Por outro lado, os pontos que não estão sobre a origem sofrem um deslocamento em relação a esta após a operação de escala. Este fato deve ser considerado na construção do modelo pois pode causar translações indesejáveis quando da criação de instâncias;
fatores de escala maiores do que 1(um) aumentam o tamanho do modelo enquanto que fatores menores que 1 e maiores que 0(zero) diminuem este tamanho. Fatores de escala negativos "invertem" o modelo em relação aos eixos coordenados

Escala em torno de um ponto arbitrário

Em diversas aplicações é necessário fazer a alteração do tamanho de um modelo com relação a pontos diferentes da origem do SRO. A este ponto, em geral, dá-se o nome de Ponto de Referência(PR).

Tomando PR, de coordenadas (x,y), como ponto em relação ao qual se deseja "escalar" um objeto e PO, de coordenadas (xo,yo), um ponto qualquer do modelo, o procedimento é o seguinte:

a)aplicar sobre PO a translação que seria necessária caso estivéssemos transladando PR para a origem:

xa= xo - xr
ya = yo - yr

b)aplicar sobre o ponto obtido a escala desejada:

xb= xa * EX
yb = ya * EY

c)desfazer a translação realizada no passo a):

xu= xb + xr
yu = yb + yr

(xu,yu) ponto no universo

Unindo este três passos em uma única fórmula tem-se:

xu= (xo-xr) * EX + xr
yu = (yo-yr) * EY + yr

Transformação de Rotação

A rotação define a orientação do modelo no universo.

A fórmula de rotação de um ponto (xo,yo) de um ângulo de 'ang' é dada por:

xu := xo * cos (ang) - yo * sin (ang)
yu:= yo * cos (ang) + xo * sin (ang)

Nesta fórmula deve-se dar especial atenção ao fato de que a maioria das linguagens possuem funções trigonométricas operando em radianos.

Da mesma forma que ocorre com a transformação de escala a rotação também se processa em torno da origem. Assim sendo, é importante considerar isto na criação do modelo para evitar translações indesejáveis.

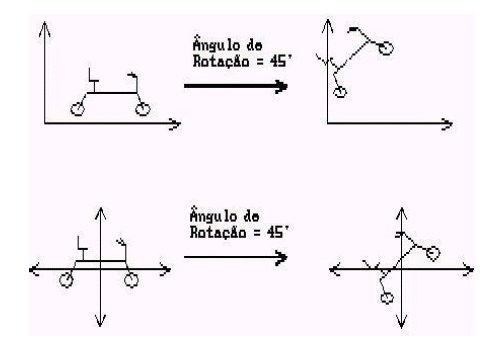
Figura - Translações indesejáveis na rotação

Rotação em torno de um ponto arbitrário

Em várias aplicações é necessário "rotacionar" um modelo em relação a pontos diferentes da origem do SRO.

Tomando um ponto de referência, de coordenadas (x,y), como ponto em relação ao qual se deseja girar um objeto e PO, de coordenadas (xo,yo), um ponto qualquer do modelo, o procedimento é o seguinte:

a)aplicar sobre PO a translação que seria necessária caso estivéssemos transladando PR para a origem:

xa= xo - xr
ya = yo - yr

b)aplicar sobre o ponto obtido a rotação desejada:

xb := xa * cos (ang) - ya * sin (ang)
yb:= ya * cos (ang) + xa * sin (ang)

c)desfazer a translação realizada no passo a):

xu= xb + xr
yu = yb + yr

(xu,yu) ponto no universo

Unindo este três passos em uma única fórmula tem-se:

xu := (xo-xr) * cos (ang) - (yo-yr) * sin (ang) + xr
yu := (yo-yr) * cos (ang) + (xo-xr) * sin (ang) + yr

MATRIZES DE TRANSFORMAÇÃO GEOMÉTRICA

Conforme é visto em disciplinas de geometria analítica é possível representar as transformações geométricas de rotação, translação e escala, em forma de matrizes. Esta forma de representação tem como vantagem básica permitir que em uma única matriz seja representada a combinação de várias transformações.

As matrizes de transformação são as seguintes:

Matriz de Translação MT

Matriz de Escala ME

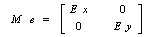
Matriz de Rotação MR

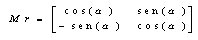
Para que as transformações sejam realizadas as coordenadas dos pontos devem ser dispostas numa matriz-linha e esta deve ser operada(multiplicada ou somada) com a matriz de transformação. A matriz de coordenadas MC deve ter a seguinte configuração: MC = [x y].

As fórmulas para a realização das transformações são as seguintes:

Translação : MC + MT

Escala : MC * ME

Rotação : MC * MR

Combinação das transformações

A principal motivação do uso da representação matricial das transformações geométricas, conforme foi mencionado, é a possibilidade de combinar as matrizes de rotação e escala em uma única matriz e posteriormente multiplicar a matriz resultante pela matriz de coordenadas. Esta combinação se dá através da simples multiplicação das matrizes MR e ME.

O inconveniente desta abordagem é que a matriz de translação não pode ser combinada com as demais, exigindo um tratamento diferenciado. Isto se deve ao fato de que a translação não é efetuada por uma multiplicação de matrizes e sim por uma soma.

Coordenadas homogêneas

Com objetivo de permitir que quaisquer das três transformações sejam realizadas com multiplicações e, com isto, tornar possível a combinação de todas elas numa única matriz foi criado o conceito de coordenadas homogêneas.

Com o uso desta técnica a configuração das matrizes apresentadas acima fica da seguinte forma:

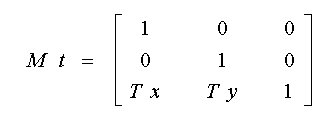
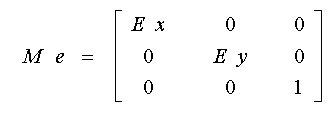
Já as fórmulas para a realização das transformações tornam-se todas multiplicações:

Translação : MC * MT

Escala : MC * ME

Rotação : MC * MR

A matriz linha resultante das operações terá sempre 3 colunas, onde a 3ª deve ser ignorada.

Para criar uma matriz única, que represente mais de uma transformação basta multiplicar as matrizes correspondentes a estas operações.

COMUTATIVIDADE DAS TRANSFORMAÇÕES GEOMÉTRICAS

Um ponto importantíssimo a ser levado em conta no procedimento de criação de matrizes únicas para representar mais de uma transformação é o problema da comutatividade. Ou seja, a ordem em que as matrizes são multiplicadas para criar um transformação única.

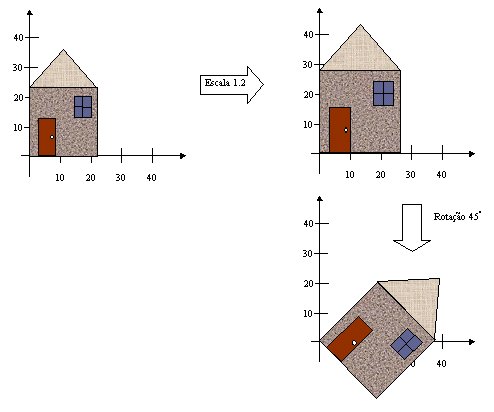
As transformações de rotação e escala são comutativas entre si, como pode ser visto na figura a seguir.

Figura - Comutatividade da Rotação e da Escala

Por outro lado, o mesmo não ocorre com a translação que não é comutativa com as outras transformações.

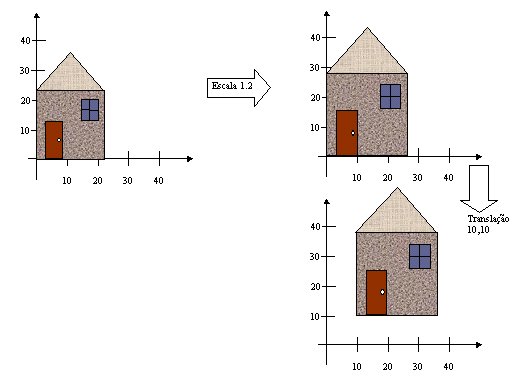
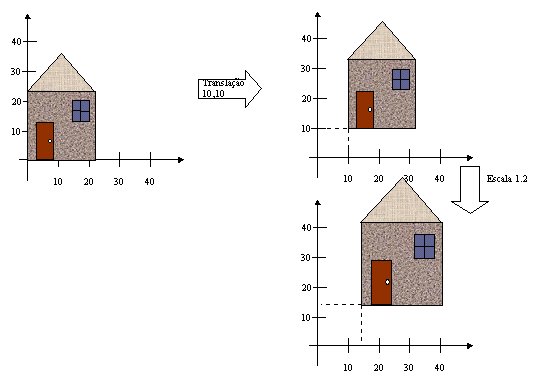
Figura - Não Comutatividade da Translação com a Escala