Sejam os ponto P1 (x1, y1) e P2 (x2, y2), a distância "d" entre P1 e P2 pode ser calculada por:

Dados os pontos P1 (x1, y1) e P2 (x2, y2) as principais formas da equação da reta suporte do segmento que liga P1 e P2 são as seguinte:

Forma explícita

Forma explícita

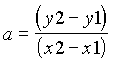Forma Implícita

Forma paramétrica

A forma paramétrica da reta baseia-se no fato de que qualquer ponto sobre o segmento de reta que liga P1 e P2 pode ser obtido por uma ponderação(média ponderada) dos pontos P1 e P2. Na qual o peso do ponto Pi (i=1,2) é tanto maior quanto mais próximo se está dele.

Tomando, por convenção, um parâmetro "t" com valor 0 no extremo correspondente a P1 e com valor 1 no extremo correspondente a P2, é possível chegar ao diagrama abaixo:

P2

. t = 1

.

P1

t = 0

A partir da observação do desenho acima é possível esquematizar a variação dos pesos de P1 e de P2 através dos seguintes gráficos:

^ Variação do Peso de P1 ^ Variação do Peso de P2

+ +

¦ ¦

¦ ¦

¦ ¦

¦ ¦

¦ ¦

¦ ¦

¦ ¦

¦ ¦

+-----------+-> +-----------+->

0 1 t 0 1 t

Dos quais se conclui que :

Peso de P1 = (1-t)

Peso de P2 = t

Fazendo-se a média ponderada de P1 e P2 tem-se:

+----------------------------------+

¦ ¦

¦ (1-t) * P1 + t * P2 ¦

¦ P = ----------------------- ¦

¦ (1-t) + t ¦

¦ ¦

+----------------------------------+

+--------------------------+

¦ ¦

¦ P = P1 * (1-t) + P2 * t ¦

¦ ¦

+--------------------------+

ou

+--------------------------+

¦ ¦

¦ P = P1 + (P2 - P1) * t ¦

¦ ¦

+--------------------------+

onde, o parâmetro "t" varia entre 0 e 1.

O que equivale a

+--------------------------+

¦ ¦

¦ x = x1 * (1-t) + x2 * t ¦

¦ ¦

¦ y = y1 * (1-t) + y2 * t ¦

¦ ¦

+--------------------------+

Um vetor V pode ser definido como um segmento de reta orientado. Para calcular as componentes de um vetor com inicio no ponto A e final no ponto B faz-se:

A: (xa, ya) B: (xb, yb)

V = B - A

V = (xb-xa, yb-ya)

B

.

.

A

8.4 MþDULO DE UM VETOR

O módulo de um vetor V1(x1, y1) fornece seu tamanho.

Representa-se "módulo" por duas barras verticais em torno do nome do vetor. O cálculo do módulo de V1(x1,y1) é dado por:

+-----------------------------------+

¦ ¦

¦ ---------------- ¦

¦ / ¦

¦ |V1| = \/ x1² + y1² ¦

¦ ¦

¦ ¦

+-----------------------------------+

O produto escalar entre dois vetores V1 e V2 é dado por:

V1: (x1, y1) V2: (x2, y2)

+------------------------------------------+

¦ ¦

¦ Prod. Esc. = x1*x2 + y1*y2 ¦

¦ ¦

¦ ou ¦

¦ ¦

¦ Prod. Esc = |V1| * |V2| * cos(alfa) ¦

¦ ¦

+------------------------------------------+

onde

alfa = ângulo entre os dois vetores

O produto vetorial entre dois vetores V1 e V2 é dado por:

V1: (x1, y1, z1) V2: (x2, y2, z2)

| i j k |

Prod. Vetorial = | x1 y1 z1 |

| x2 y2 z2 |

i = (y1 * z2) - (z1 * y2)

j = (z1 * x2) - (x1 * z2)

k = (x1 * y2) - (y1 * x2)

O produto vetorial entre V1 e V2, nesta ordem, define um vetor perpendicular a V1 e V2, conforme a figura 8.1a. Se a ordem do produto for invertida o vetor resultante terá seu sentido invertido(figura 81.b).

[cg8_1.pix]

D A

D

C

B

Onde,

A : (xa, ya) B : (xb, yb) C : (xc, yc) D : (xd, yd)

+----------------------------+

¦ ¦

¦ (V1 . V2) ¦

¦ ANG = ACOS ----------- ¦

¦ |V1|*|V2| ¦

¦ ¦

+----------------------------+

Onde

V1 = B - A -->> (xb-xa, yb-ya)

V2 = D - C -->> (xd-xc, yd-yc)

V1 . V2 -> (produto escalar de V1 por V2) =>> x1*x2 + y1*y2

Dado um segmento de reta R com extremidade nos pontos A(xa, ya) e B(xb, yb) e um ponto P1 de coordenadas (x1, y1) a distância entre a P1 e R é definida pelo comprimento do segmento de reta S, perpendicular a R e com extremos em P1 e no ponto de intersecção de R com S.

.B

.P1

. A

+----------------------------+

¦ ¦

¦ Ax1 + By1 + C ¦

¦d = ---------------------- ¦

¦ (A*A + B*B) ^ (1/2) ¦

¦ ¦

+----------------------------+

onde A, B e C são os coeficientes da equação geral da reta R, conforme o item 8.2.

Dado o segmento de reta R1 de extremos nos pontos K(xk, yk) e L(xl, yl) e o segmento de reta R2 com extremos em M(xm, ym) e N(xn yn).

Dadas suas equaç¨es paramétricas:

R1 : x = xk + (xl - xk) * s

y = yk + (yl - yk) * s

R2 : x = xm + (xn - xm) * t

y = ym + (yn - ym) * t

Calcula-se "d" por:

+-----------------------------------------------------------+

¦ ¦

¦ d = (xn - xm) * (yl - ky) - (yn - ym) * (xl - xk) ¦

¦ ¦

+-----------------------------------------------------------+

se "d" for igual a zero então as linhas são paralelas. Caso contrário, o valor do parâmetro "s" na intersecção de R1 com R2 é dado por :

+-----------------------------------------------------------+

¦ ¦

¦ (xn - xm) * (ym - yk) - (yn - ym) * (xm - xk) ¦

¦ s = ------------------------------------------------- ¦

¦ d ¦

¦ ¦

+-----------------------------------------------------------+

e o valor do parâmetro "t" no mesmo ponto por:

+-----------------------------------------------------------+

¦ ¦

¦ (xl - xk) * (ym - yk) - (yl - yk) * (xm - xk) ¦

¦ t = ------------------------------------------------- ¦

¦ d ¦

¦ ¦

+-----------------------------------------------------------+

Sejam os vértices V1, V2, ..., e Vn, do polígono P, dispostos em sentido horário. Para determinar se P é côncavo ou convexo, basta fazer:

Calcular os produtos vetoriais :

(V2-V1) X (V3-V1) = 0, 0, z1

(V3-V2) X (V4-V2) = 0, 0, z2

............................

............................

(VN-Vn-1) X (V1-Vn-1) = 0, 0, zn

Onde o operador "X" indica o produto vetorial entre dois vetores.

O resultado de todos os produtos vetoriais da lista acima terão a forma (0, 0, z). Se em algum destes o valor de Z for NEGATIVO então o polígono P é CÞNCAVO. Senão, é convexo.

Na figura 8.2 pode-se observar um exemplo de polígono côncavo

OBS.:

A coordenada Z dos vértices do polígono deve ser 0(zero).

[cg8_2.pix]

Sejam os vértices V1, V2, ..., e Vn, do polígono P, dispostos em sentido horário. Para determinar se o ponto Q está dentro ou fora de P basta fazer:

Calcular os produtos vetoriais :

(V2-V1) X (Q-V1) = 0, 0, z1

(V3-V2) X (Q-V2) = 0, 0, z2

(V4-V3) X (Q-V3) = 0, 0, z3

............................

............................

(V1-Vn) X (Q-Vn) = 0, 0, zn

Onde o operador "X" indica o produto vetorial entre dois vetores.

O resultado de todos os produtos vetoriais da lista acima terão a forma (0, 0, z). Se em algum destes o valor de Z for NEGATIVO então o ponto está FORA do polígono P. Se em algum dos caso Z for 0 então o ponto Q está sobre uma das arestas de P.

OBS.:

A coordenada Z dos vértices do polígono e do ponto P deve ser 0(zero).

Sejam os vértices V1, V2, ..., e Vn, do polígono P, dispostos em sentido horário. Para determinar se o ponto Q está dentro ou fora de P faz-se:

a)cria-se um segmento de reta horizontal iniciando em Q e terminando em R, um ponto à esquerda de Q, com a coordenada "y" igual a de Q;

b)determina-se qual a aresta do polígono que cruza PQ no ponto mais próximo de Q. Suponha-se que esta aresta tenha início em P1(x1,y1) e fim em P2(x2,y2);

c)calcula-se o produto vetorial

(P2-P1) X (Q-P1)

d)se a componente Z do resultado do produto vetorial recém calculado for POSITIVA o ponto está DENTRO; se for NEGATIVA, está fora. Se for 0 (zero), Q está sobre a aresta P2-P1.

OBS:

Caso nenhuma aresta do polígono cruze a linha QR então o ponto está fora do polígono.

[cg8_3.pix]