Computação Gráfica
Processo de
Visualização Bidimensional
RECORTE
Quando
há, no universo, objetos (entidades) que ficam, total ou parcialmente, fora da
Janela de Seleção("window") definida para a visualização é preciso
não exibi-las(figura)

Figura - Exemplo de Recorte
Ao
processo de retirada dos objetos que não estão dentro da Janela de Seleção
dá-se o nome de RECORTE.
RECORTE DE RETAS
O
ponto mais importante no procedimento de Recorte é o recorte de retas. Recortar
uma reta, na verdade, em detectar quais os pontos de intersecção desta com os
lados da Janela de Seleção.
Tomando,
conforme a figura a seguir, uma Janela de Seleção com os limites inferior
esquerdo no ponto (min_x,min_y) e superior direito no ponto (max_x,max_y) e uma reta
R de (xi,yi)
a (xf,yf)
o procedimento de recorte pode ser resumido da seguinte forma:
- calcula-se a intersecção da reta R com a borda lateral esquerda da Janela de Seleção. Se a intersecção ocorrer entre os limites superior e inferior Janela de Seleção, então elimina-se o ponto mais à esquerda da reta R, trocando-o pelo ponto recém calculado;
- calcula-se a intersecção da reta R com a borda superior da Janela de Seleção(já como o novo extremo obtido no passo anterior). Se a intersecção ocorrer entre os limites esquerdo e direito da Janela de Seleção, então elimina-se o ponto mais acima da reta R, trocando-o pelo ponto recém calculado;
- calcula-se a intersecção da reta R com a borda lateral direita da Janela de Seleção(já como o novo extremo obtido no passo anterior). Se a intersecção ocorrer entre os limites superior e inferior Janela de Seleção, então elimina-se o ponto mais à direita da reta R, trocando-o pelo ponto recém calculado;
- calcula-se a intersecção da reta R com a borda inferior da Janela de Seleção(já como o novo extremo obtido no passo anterior). Se a intersecção ocorrer entre os limites esquerdo e direito da Janela de Seleção, então elimina-se o ponto mais abaixo da reta R, trocando-o pelo ponto recém calculado.
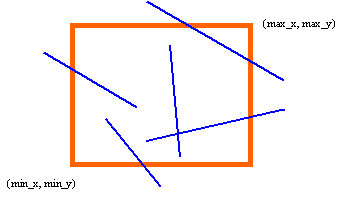
Figura - Linhas a recortar
Cálculo das intersecções
Do
algoritmo exposto acima falta, apenas, calcular a intersecção entre a reta e as
bordas da Janela de Seleção.
Chamando
o ponto de intersecção de Pi(x_int,y_int), o cálculo processa-se da
seguinte forma:
Tomando
o segmento de reta : (xi, yi) - (xf, yf)
A
Janela de Seleção : (min.x, min.y) - (max.x max.y)
Tem-se :
a) da reta com a borda da esquerda
x_int = min.x ;
m1 = (yf - yi) / (xf - xi);
y_int = yi + (min.x - xi) * m1;b) da reta com a borda da direita
x_int = max.x ;
m1= (yf - yi) / (xf - xi);
y_int = yi + (max.x - xi) * m1;c) da reta com a borda superior
m2 = (xf - xi) / (yf - yi);
x_int = xi + (max.y - yi) * m2;
y_int = max.y ;d) da reta com a borda inferior
m2 = (xf - xi) / (yf - yi);
x_int = xi + (min.y - yi) * m2;
y_int = min.y ;
Um
ponto importante nestes cálculos é o cuidado com as linhas verticais e
horizontais. No caso de linhas verticais não deve-se
calcular a intersecção com as bordas direita e esquerda. No caso de linhas
horizontais não deve-se calcular a intersecção com as bordas
superior e inferior.
ALGORITMO DE COHEN-SUTHERLAND
O
algoritmo recém apresentado opera perfeitamente no
recorte de retas. Porém, analisando-o com mais cuidado nota-se que em certos
casos o cálculo de interseção irá gerar um ponto que fica fora da Janela de
Seleção(figura). Este cálculo, portanto, é indesejável pois apenas consume
tempo de processamento sem gerar nenhum resultado útil.
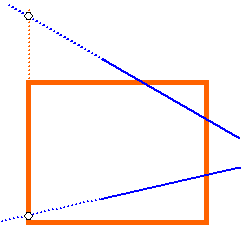
Figura - Cálculos desnecessários
Na
realidade, estes cálculos inúteis correspondem a pelo menos a metade dos
cálculos de intersecção realizados. Isto porque uma reta pode cruzar apenas
duas das bordas da Janela de Seleção. Este desperdício fica, ainda maior, nos
casos em que um dos extremos da linha(ou ambos) estão
dentro da Janela de Seleção.
Pensando
nisto, adota-se um algoritmo (Cohen-Sutherland) que tem por objetivo evitar a
execução de cálculos desnecessários.
O
primeiro passo deste algoritmo é codificar os extremos da linha a ser
recortada.
Para
a obtenção deste código o plano XY é dividido em 9 partes através das bordas da
Janela de Seleção(figura).

O
código dos pontos de cada uma das 9 áreas é formado por um número de 4 bits, da
seguinte maneira:
1º bit :
em 1 se o ponto está à esquerda da J.S.
em 0 se o ponto não está à esquerda da J.S.2º bit :
em 1 se o ponto está à direita da J.S.
em 0 se o ponto não está à direita da J.S.3º bit :
em 1 se o ponto está abaixo da J.S.
em 0 se o ponto não está abaixo da J.S.4º bit :
em 1 se o ponto está acima da J.S.
em 0 se o ponto não está acima da J.S.
Duas
possíveis estruturas de dados para armazenar estes códigos são:
code1, code2 : array [1..4] of boolean;
ou
code1, code2 : integer;
Usando
a segunda forma de representação o cálculo do código de um ponto pode ser feito
pela seguinte função:
Function Codifica(x,y:real) : integer;
Var
cod: integer;Begin
cod := 0;
If (y > Max_Y) {Ponto acima da Janela de Seleção}
Then cod := 1
Else if (y < Min_Y){Ponto abaixo da Janela de Seleção }
Then cod := 2;if (x > Max_X) { Ponto a direita da Janela de Seleção }
Then cod := cod + 4
Else if (x < Min_X) { Ponto à esquerda da Janela de Seleção }
Then cod := cod + 8;Codifica := cod;
End;
A
vantagem do uso deste tipo de codificação para os extremos da linha a ser
recortada reside no fato de que é possível, mesmo antes de iniciar o cálculo das intersecções,
tomar algumas decisões sobre a linha:
a)Decidir se a linha está TODA DENTRO da Janela de Seleção e desta forma pode ser exibida sem recorte. Para obter esta informação basta verificar se ambos os códigos tem valor 0000. Ou então fazer um OR dos dois códigos, se der 0, a linha está dentro.
Exemplos de código:
1)
dentro := TRUE;
for i := 1 to 4
do if (code1[i] or code2[i]) = TRUE
then dentro := FALSE;
if (dentro = TRUE)
then //linha toda dentro, não necessita de recorte2)
if (code1 OR code1) = 0
then // linha toda dentro, não necessita de recorte
b)Decidir se a linha está TODA FORA da Janela de Seleção e desta forma não ser exibida. Para obter esta informação basta realizar um AND dos códigos, se o resultado for diferente de 0 a linha está toda fora.
Exemplos de código:
1)
fora := FALSE;
for i := 1 to 4
do if code1[i] and code2[i]
then fora := TRUE;
if (fora = TRUE)
then //linha toda fora, não deve ser exibida2)
if (code1 AND code2) <> 0
then //linha toda fora, não deve ser exibida
Nos
casos em que nenhuma das providências acima puder ser adotada, o algoritmo
prossegue nos seguinte passos(assuma que a linha é
definida pelos pontos extremos P1 e P2):
1)
Calcule os códigos de P1 e de P2;
Se P1 estiver fora da J.S
então siga para o passo 2
senão troque P1 com P2;
2)
Verifique, pelo código de P1, se este encontra-se à esquerda da J.S. (1º bit em
1).
Se não estiver siga para o passo 3;
Se estiver
então calcule Pi, o ponto de intersecção da reta P1-P2 com o lado esquerdo da J.S.
coloque Pi em P1 (P1 := Pi)recalcule o código de P1
siga para o passo 6;
3)
Verifique, pelo código de P1, se este encontra-se à direita da J.S. (2º bit em
1).
Se não estiver siga para o passo 4;
Se estiver
então calcule Pi, o ponto de intersecção da reta P1-P2 com o lado direito da J.S.
coloque Pi em P1 (P1 := Pi), recalcule o código de P1
siga para o passo 6;
4)
Verifique, pelo código de P1, se este encontra-se acima da J.S. (3º bit em 1).
Se não estiver siga para o passo 5;
Se estiver
então calcule Pi, o ponto de intersecção da reta P1-P2 com o lado de cima da J.S.
coloque Pi em P1 (P1 := Pi), recalcule o código de P1
siga para o passo 6;
5)
Verifique, pelo código de P1, se este encontra-se abaixo da J.S. (4º bit em 1).
Se não estiver siga para o passo 6;
Se estiver
então calcule Pi, o ponto de intersecção da reta P1-P2 com o lado de baixo da J.S.
coloque Pi em P1 (P1 := Pi), recalcule o código de P1
siga para o passo 6;
6)
Verifique se a nova linha P1-P2 está toda dentro ou toda fora da J.S.
Recalcule o código de P1;
Se (P1 OR P2) = 0
então linha recortada está em P1-P2
encerra o algoritmo.
senão Se (P1 AND P2) <> 0
então linha está toda fora da J.S;
encerra o algoritmo.
senão volta ao passo 1.


