---

Computação Gráfica
Processo de Visualização Bidimensional

MAPEAMENTO

Prof. Márcio Sarroglia Pinho

INTRODUÇÃO

Após o processo de Instanciamento e de Recorte, nas coordenadas resultantes não são(em geral) compatíveis com as coordenadas da tela.

Normalmente quando se cria um modelo as informações gráficas armazenadas neste, (coordenadas, tamanhos, cores, espessuras, etc.) dizem respeito à aplicação e não ao dispositivo que está sendo usado.

Por exemplo, quando aplicação é um sistema de desenho de plantas, as dimensões de uma porta ou de uma parede, são armazenadas em metros ou polegadas e não em pontos de tela. Outro exemplo deste fato são sistemas de traçado de curvas, por exemplo, no caso do traçado da função "seno" os valores sobre o eixo X variam entre 0 e 2 PI e sobre Y de -1 até +1. Se tentarmos traçar estes valores diretamente na tela teremos problemas, pois serão vistos apenas alguns pontos no canto superior esquerdo da mesma.

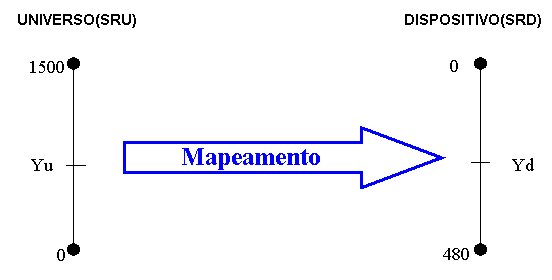
Para permitir a visualização deste tipo de entidades(modelos) faz-se necessário realizar uma conversão dos valores do modelo para valores compatíveis com as dimensões da tela. A esta conversão dá-se o nome de MAPEAMENTO. Um exemplo onde é necessária uma operação de mapeamento pode ser visto na figura a seguir. Neste exemplo o objeto original(modelo) está descrito em um sistema de coordenadas de dimensões muito grandes para a tela e além disto os sistemas tem o eixo Y crescendo em direções opostas.

Para realizar o mapeamento entre estes dois Sistemas de Referência tomemos um ponto "Pu" de coordenadas (Xu,Yu), no SRU e tentemos obter seu correspondente (Xd, Yd) no SRD, ou seja na tela.

Os dados para efetuar a conversão, são os seguintes:

	Limites do SRU	Limites do SRD
Mínimo	(0,0)	(0,0)
Máximo	(1000,1500)	(640,480)

Iniciando pela componente X temos, de acordo com o diagrama abaixo,

de onde deduz-se a relação:

Xd - 0      640 - 0
-------- = ---------
Xu - 0     1000 - 0

da qual se pode concluir que,

Xu * 649
Xd = -----------
     1000  

Para a componente Y o processo é análogo, alterando-se apenas os limites dos sistemas de referência, E ATENTANDO PARA O FATO DE QUE O EIXO "Y" CRESCE EM SENTIDOS OPOSTOS NOS DOIS SISTEMAS.

de onde deduz-se a relação

Yd - 480    0 - 480
--------- = ----------
Yu - 0     1500 - 0

da qual se pode concluir que,

Yu * (-480)
Yd = ----------- + 480
 1500  

JANELA DE SELEÇÃO e JANELA DE EXIBIÇÃO

Quando definimos que a área de trabalho da aplicação vai de (0,0) a (1000,1500), estamos selecionando a região do plano cartesiano com a qual desejamos trabalhar. A esta região dá-se o nome de JANELA DE SELEÇÃO ou WINDOW. Dependendo da aplicação, podemos diminuir esta área, num porcesso conhecido como ZOOM. Esta modificação é em geral definida pelo usuário da aplicação.

Quando definimos que a área de exibição, dentro da tela, vai de (0,0) a (640, 480), estamos especificando a JANELA DE EXIBIÇÃO ou VIEWPORT. A modificação de uma Viewport é, em geral, definida pelo programador da aplicação.

Estas regiões, dependendo da aplicação, ou mesmo do momento, podem variar. A fim de tornar as fórmulas de mapeamento genéricas quanto às Janela de Seleção/Exibição escolhidas, basta definir variáveis que representem as coordenadas de seus cantos. Por exemplo:

TYPE

XYR = Record
x,y : real;
End;

VAR

MIN_SEL, (* canto inferior esquerdo da Jan. de seleção *)
MAX_SEL : XYR; (* canto superior direito da Jan. de seleção *)
MIN_EXB (* canto inferior esquerdo da Jan. de exibição *)
MAX_EXB : XYR;(* canto superior direito da Jan. de exibição *)

A partir disto, as funções de mapeamento ficam da seguinte forma:

(Xu - MIN_SEL.X) * (MAX_EXB.X - MIN_EXB.X)      
Xd = ------------------------------------------------- + MIN_EXB.X
MAX_SEL.X - MIN_SEL.X

(Yu - MIN_SEL.Y) * (MIN_EXB.Y - MAX_EXB.Y)      
Yd = ------------------------------------------------- + MAX_EXB.Y
MAX_SEL_.Y - MIN_SEL.Y